Let's consider a stainless steel pipe transporting saturated steam. The pipe inlet condition is 6 barg at 165 degrees C with a fixed flow rate at the outlet of the pipe 1 kg/h (0.0002778 kg/s).
What we can sometimes see is that even if you set a low flow rate for a long un-insulated pipe with a low outside ambient temperature, the outlet fluid temperature is almost the same as the inlet temperature (165 deg. C). What happens in this scenario?
In addition to the presence of two phase flow, what we also need to consider here is the laminar flow regime and inside film coefficient of the pipe. The inside film coefficient of a pipe represents the resistance to heat flow. The fundamentals of heat transfer change considerably when we encounter low flow conditions in the laminar region. This affects the resultant inside film coefficient considerably which of course has a knock on effect on the heat transfer.
The equations used to calculate the inside film resistance (using Nusselt number) are as follows:
Turbulent Flow Regime:
We use the Dittus-Boelter equation (NuD = 0.023ReD 4/5 Prn) and the heat transfer coefficient is calculated from h = kw/DH * Nu where kw is the thermal conductivity of the fluid and DH is the hydraulic diameter.
Laminar Flow Regime:
For laminar flow, we use h = kw/DH * (3.65 + 0.0668 * Re * Pr * DH / L) / (1.04 + (Re * Pr * (L/dH))^2/3).
Transition Flow Regime:
For flow in the transition region, we use the term defined above for laminar flow, however, we will now assign as X - i.e. X = kw/DH * (3.65 + 0.0668 * Re * Pr * DH / L) / (1.04 + (Re * Pr * (L/dH))^2/3). For heat transfer in this region, we then use h = X + 0.023 * kw/DH * Re^4/5 * Pr^1/3)-X) * ((Re-2000)/8000).
Lets take a look at an example of a 1.0 M long 22 mm pipe with a flow rate of 1 kg/h (0.0002778 kg/s). The calculation results are as follows:
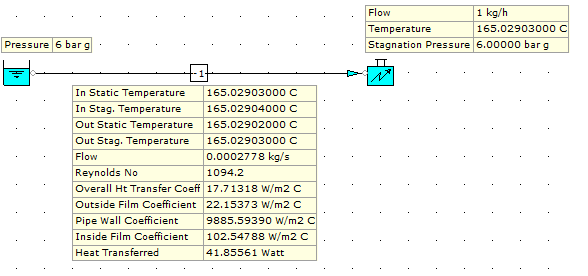
As we can see, the Reynolds Number (Re) is 1094.2, i.e. the laminar region which affects Nusselt Number.
If we then take a 1 km example of the same pipe, the Re number is also 1094.2 as the properties such as velocity, viscosity, density, specific heat capacity etc are essentially the same. The system is once again in the laminar region. The results of the 1 km model are as follows:
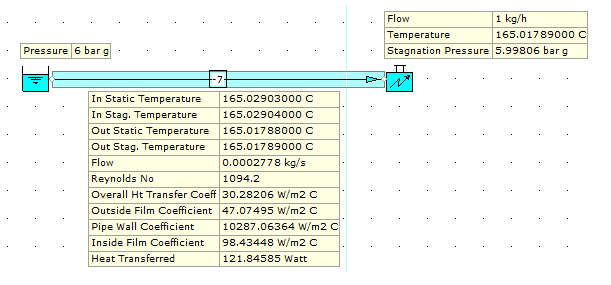
The main difference in this system is not so much the temperature, but the vapor quality. The vapor quality at the outlet of the 1.0 M long pipe is 0.9999 (99.9%). However, the vapor quality at the outlet of the 1.0 kM long pipe is 0.78454 (78.4%). This represents a 21.5% difference over a considerable length of pipe and as such, a considerable change when considering the pipe volume.
Although it may seem counter-intuitive, the net change in the system characteristic is in the vapor quality parameter.