FluidFlow

Equipment Sizing Handbook

© Flite Software NI Ltd

1  Introduction        2

2  Pipe Sizing.        3

2.1  Economic Velocity.        3

2.2  By Velocity.        9

2.3  By Pressure Gradient.        9

3  Control Valve Sizing.        11

4  Pump Sizing.        14

5  Orifice Plate Sizing.        16

6  Auto-Equipment Sizing – Cooling Water Plant        18

7  Conclusion        23

1. Introduction

FluidFlow software offers a fast and effective approach to automatically sizing piping and associated equipment. This helps accelerate the design process saving the designer both time and capital cost. Furthermore, the correct sizing of equipment is crucial in terms of developing efficient system designs as well as optimizing capital installation cost.

Table 1 below describes the elements which can be automatically sized using FluidFlow software.

Table 1

This document will outline the various approaches you can take to automatically sizing your piping and associated equipment. Each piping element will initially be considered in isolation of a system and finally, a sample system will be designed with piping and associated equipment automatically sized.

2. Pipe Sizing.

FluidFlow allows you to automatically size a pipe or duct based on any of the following three methods; 1) Economic Velocity, 2) By Velocity and 3) By Pressure Gradient.

1. Economic Velocity.

The economic velocity is a function of the physical properties of the fluid being transported, the pipe materials, various capital and installation costs, the operating hours per annum etc. This value is calculated automatically by FluidFlow using the values and constants stored in the pipe sizing database.

Economic velocity is changing (generally decreasing) with time, particularly as energy costs have increased rapidly in recent times. These values are updated regularly by Flite Software NI Ltd which is one of many reasons why it is important keep your software current.

Economic Velocity is the default Sizing Model for a pipe is shown in Figure 2.1.1.

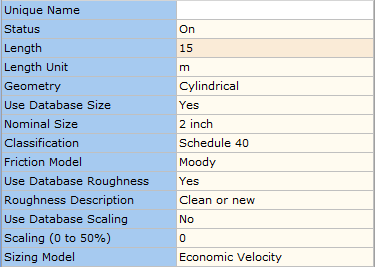
Figure 2.1.1: Economic Velocity Sizing Model.

If you proceed with Economic Velocity as the Sizing Model, the software will determine the Exact Economic Size corresponding to the economic velocity which is automatically calculated by the software. This information can be viewed in the Results tab of the Data Palette.

The simplest way to demonstrate this is to consider a simple example.

We wish to transport 100 m3/h of water at 15 oC along a 15 M long steel pipeline. The design pressure at the outlet of this pipeline is 2 bar g.

Step 1: Build a Model of the System.

A model of this system has been developed as outlined in Figure 2.1.2.

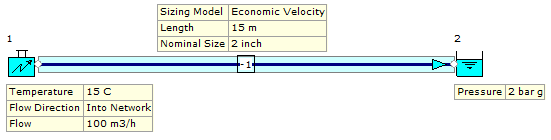Figure 2.1.2: 15.0 M Long Water System Model.

This model has been created using steel pipework.

Step 2: Define the Design Parameters for the nodes.

When building a model, the software provides default data for each node/element. This data can be viewed on the Input tab of the Data Palette.

The data entry for the inlet boundary node is shown in Figure 2.1.3.

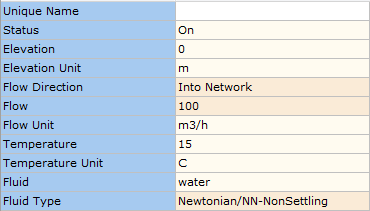Figure 2.1.3: Data Entry for Inlet Boundary.

The data entry for the outlet boundary node is shown in Figure 2.1.4.

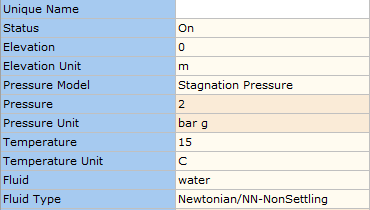Figure 2.1.4: Data Entry for Outlet Boundary.

Finally, the data entry for the pipe as shown in Figure 2.1.5.

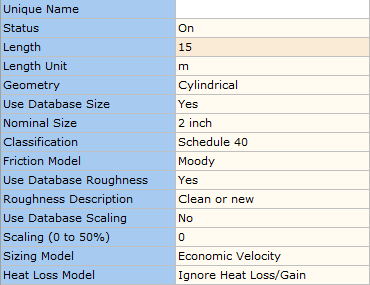Figure 2.1.5: Data Entry for the Pipe.

You may notice that the default Nominal Size for steel pipes is 2 inch and the Classification is Schedule 40. We have simply retained this default data entry as we are going to allow the software to calculate the most economic pipe size for us.

Step 2: Calculate the Model.

When we calculate the model, the flow direction is shown for each pipe in the system and we can view the results by clicking the pipe on the flowsheet followed by the Results tab on the Data Palette.

If you calculate your model at this stage, you will notice the pipe element (node -1) is highlighted in red which means we have a warning message which we can view on the Messages tab on the Data Palette.

Figure 2.1.6 shows the calculated results with the pipe shows highlighted in red.

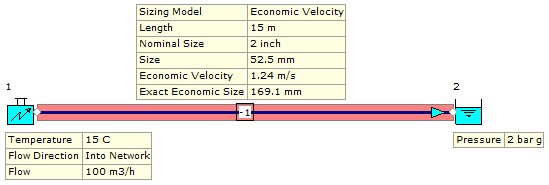Figure 2.1.6: Calculated System.

Figure 2.1.7 shows we have one warning message for the pipe indicating we have a high flow velocity.

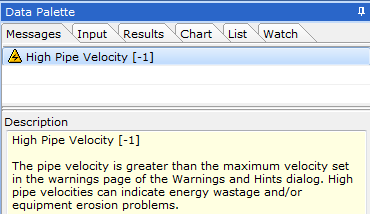Figure 2.1.7: Warning Messages.

We can new review the calculated results in detail by selecting the pipe on the flowsheet followed by the Results tab on the Data Palette.

The results are shown in Figure 2.1.8. We can see that the system has solved with the default pipe size of 2 inch (52.5mm) which returns a flowing velocity of 12.83 m/s which is considered high for a liquid system. However, we can also see that the calculated Economic Velocity is 1.24 m/s yielding an Exact Economic Size of 169.1 mm.

Figure 2.1.8: Pipe Results.

As our pipe is just 52.5mm, we can see instantly that we need to increase to a standard pipe size/diameter close to 169.1mm in order to achieve a more economic design velocity near 1.24 m/s.  

As 169.1mm equates to 6.66 inches, we can try modeling a 6 inch pipe and review the calculated velocity. From the Input, change the Nominal Size by clicking the grey box to the right hand side of the field. Figure 2.1.9 gives an overview of the Nominal Size data entry field.

Figure 2.1.9: Nominal Pipe Size.

This opens the steel pipe database. Expand the 6 Inch field to view the classifications and select schedule 40. Figure 2.1.10 shows the steel pipe database including available sizes.

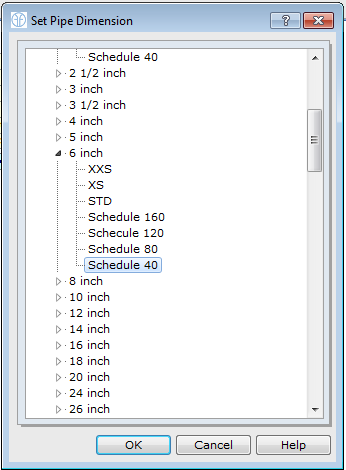Figure 2.1.10: Steel Pipe Database.

Select ok to confirm this new pipe size. Recalculate the model and you should notice the red warning message has disappeared and the flowing velocity is now 1.49 m/s which is more in line with an economic design.

Note, if capital installation cost is an issue, you can also consider other pipes sizes. For instance, a 5 inch schedule 40 pipe returns a flowing velocity of 2.15 m/s and a 4 inch pipe a velocity of 3.38 m/s. This allows you to quickly consider efficient design alternatives.

Economic velocity is a useful guide for pipe sizing, helping engineers develop efficient and economic plant designs. It is however important to give consideration to the type of system you are designing. For instance, you would not use this criteria to size pipes where two-phase (liquid-gas) flow is present, or where plant operation is intermittent, or where materials can degrade at high velocities or for non-Newtonian flows.

2. By Velocity.

If you select By Velocity, Figure 2.2.1 shows the additional data entries that are required for the pipe(s) in the model.

Figure 2.2.1: By Velocity Pipe Sizing Model.

Choosing By Velocity allows you to set the design velocity for your pipes. When you calculate your piping system, you will see in your results the Exact Velocity Size which is the exact pipe diameter required based on your defined velocity. Figure 2.2.2 shows the results provided when using this pipe sizing approach (based on the previous economic sizing example case and a design velocity of 2.5 m/s).

Figure 2.2.2: By Velocity Pipe Sizing Results.

We can see at a glance that a pipe size of approximately 118.9 mm (4.68 inches) would be required to achieve this design velocity. We can therefore consider a 5 inch pipe for this system. A 5 inch schedule 40 pipe yields a velocity of 2.15 m/s. As 5 inch may not be a standard readily available pipe size, you can quickly consider alternative sizes and review the velocity in each case.

3. By Pressure Gradient.

If you select By Pressure Gradient, Figure 2.3.1 shows the additional data entries that are required for the pipe(s) in the model. Note, you can set your desired pressure gradient and associated units.

Figure 2.3.1: By Pressure Gradient Pipe Sizing Model.

Choosing By Pressure Gradient allows you to set the design pressure gradient for your pipes. When you calculate your piping system, you will see in your results the Exact Pressure Gradient Size which is the exact pipe diameter required based on your defined gradient. Figure 2.3.2 shows the results provided when using this pipe sizing approach (based on the previous economic sizing example case and a design pressure gradient of 360 Pa/m).

Figure 2.3.2: By Pressure Gradient Pipe Sizing Results.

We can see at a glance that a pipe size of approximately 125.5 mm (4.94 inches) would be required to achieve this design gradient. We can therefore consider a 5 inch pipe for this system. A 5 inch schedule 40 pipe yields a velocity of 2.15 m/s. As 5 inch may not be a standard readily available pipe size, you can quickly consider alternative sizes and review the velocity in each case.

Note, when sizing ductwork using any of these three models, the software will calculate the required duct diameter. If you wish to develop a ductwork system with a rectangular geometry, you will need to determine the height and width of duct required and enter these values into the Input tab of the Data Palette for each section of ductwork. There are various literature sources which provide tables of equivalent dimensions for circular ductwork, such as the ASHRAE Guides & CIBSE Guide C.

3. Control Valve Sizing.

Engineers can automatically size flow and pressure control valves to ISA Standard: ISA-75.01.01-2007.

The following example case is derived from Example 1, Appendix E of ISA-75.01.01-2007. This system is based on incompressible flow of fluid (water) with a temperature of 363 K, density of 965.4 kg/m3, inlet and outlet absolute static pressure of 680 and 220 kPa a respectively and a flow rate of 360 m3/h.

Step 1: Build a Model of the System.

A model of this system has been developed as outlined in Figure 3.1.1. This model includes a flow control valve as we know the design flow rate for the system based on available data.

Figure 3.1.1: Flow Control Valve System Model.

Step 2: Define the Design Parameters for the nodes.

The data entry for the inlet boundary node is shown in Figure Figure 3.1.2.

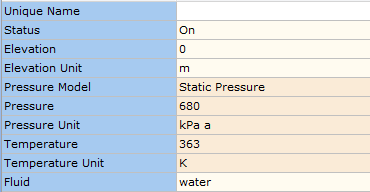Figure 3.1.2: Inlet Boundary – Input Data.

The data entry for the outlet boundary node is shown in Figure Figure 3.1.3.

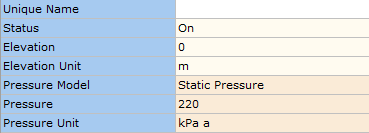Figure 3.1.3: Outlet Boundary – Input Data.

As we know the design flow rate for the system, we can set this parameter at the flow control valve. The data entry for this valve is as shown in Figure 3.1.4.

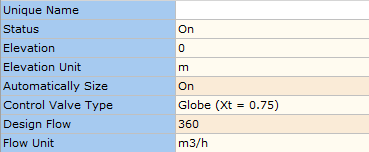Figure 3.1.4: Control Valve – Input Data.

As we can see in Figure 3.1.4, the value for Xt is set to 0.75 as per the ISA Standard example. The connected pipes are also set to 150mm in line with the worked example.

When we solve this system, FluidFlow calculates a Kv of 165.088 m3/h/bar whereas the hand calculation notes a Cv value of 165 m3/h/bar. The results are almost identical.

An overview of the FluidFlow results are shown in Figure 3.1.5.

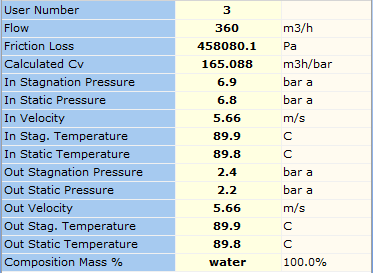Figure 3.1.5: Control Valve Results.

You can also model vendor specific valves in your model. Setting the Automatically Size function to OFF allows you to model a manufacturer’s valve from the database. Figure 3.1.6 shows the results of a calculation which utilizes the globe parabolic plug valve as described in the ISA Standard. The results clearly show the % opening of the valve based on the design flow rate, in this case, the control valve would be 68 % open in order to achieve the design conditions.

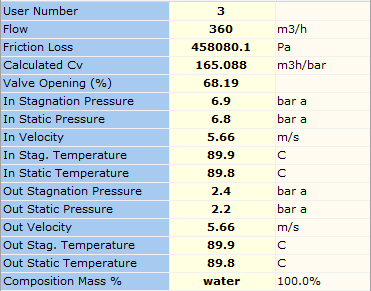Figure 3.1.6: Vendor Control Valve Results.

4. Pump Sizing.

Pumps can be automatically sized based on either a design flow rate or design pressure rise across the system.

The example in Figure 4.1.1 demonstrates both approaches. Both models show a pumped system transporting water at 15oC and 1 atm pressure to an outlet with a design pressure of 1 bara via a network of 50 mm pipes. The pump in the top model is sized based on a design flow rate of2.7754 kg/s. Based on the design conditions and engineering conditions which apply, the calculated duty pressure rise is 117675.3 Pa (12.0 m fluid).

The bottom model is an identical match however, the pump sizing criteria set to design pressure rise which is set to 117675.3 Pa. When the simulation is completed, we can see the resultant flow rate calculate is 2.7754 kg/s (10 m3/h) which of course is identical to the first system.

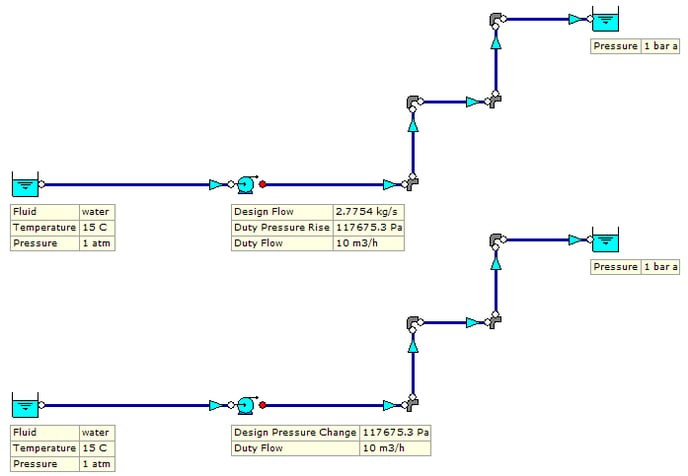
Figure 4.1.1: Pump Sizing Models.

An overview of some pump results for automatically sized pumps are shown in Figure 4.1.2. Note, when we model a vendor pump in our system, the software also calculates the duty power requirement, efficiency and NPSHr. You can also model changes in pump speed and impeller diameter thus helping you optimise your system performance.

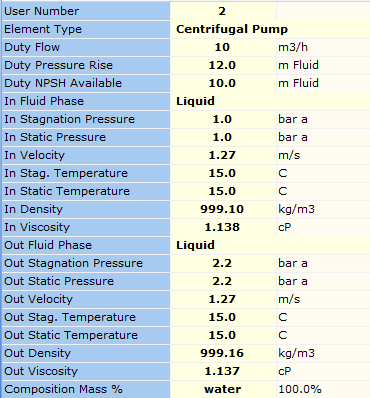Figure 4.1.2: Automatically Sized Pump Results.

Note, FluidFlow allows you to automatically size centrifugal pumps, fans and compressors based on a design flow rate or duty pressure rise. PD pumps and Rotating PD pumps can be automatically sized based on a design system flow rate.

5. Orifice Plate Sizing.

A comparison study has been completed on a test model for flange tap loss based on ISO 5167. The design pipe diameter is 300mm with an orifice size of 120mm. The benchmark hand calculation is based on a fluid density of 1000 kg/m3 and viscosity of 1.2927 centipoise. The hand calculation also quotes a velocity of 2.46 m/s, a flow rate of 0.0279m3/s and a flange tap loss of 8200 Pa.

Figure 5.1.1 shows the model of the system developed in FluidFlow. The orifice plate has been automatically sized based on the design flow rate noted of 0.0279 m3/s.  

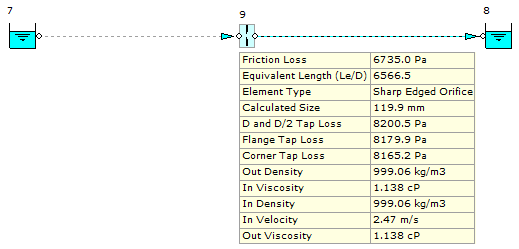Figure 5.1.1: Automatically Sized Orifice Plate.

Based on the available data, FluidFlow has calculated an orifice size requirement of 119.9mm or 120mm which matches the example hand calculation. The software also calculated a flange tap loss of 8179.9 Pa and a velocity of 2.47m/s. It can therefore be seen that the results compare well. Subtle differences can be attributed to the differences in fluid density 999.06 kg/m3, viscosity (1.138 centipoise) etc. Figure 5.1.2 shows some of the results available for an automatically sized orifice plate.

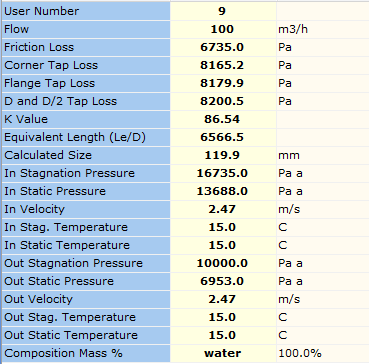Figure 5.1.2: Automatically Sized Orifice Plate Results.

The results for flange tap loss, D and D/2 loss, corner tap loss along, friction loss and associated k value are all automatically calculated for orifice plates.

Note, this orifice plate can also be automatically sized based on a design pressure drop.

Finally, we can model an actual orifice in the system. Let’s model the size of 119.9 mm as determined earlier. Figure 5.1.3 provides an overview of the results.

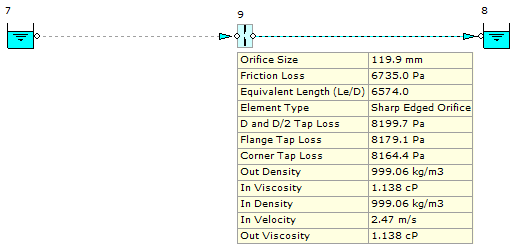
Figure 5.1.3: 119.9mm Orifice Plate Model.

The results from this calculation are a close match for the initial run where the orifice plate was automatically sized.

6. Auto-Equipment Sizing – Cooling Water Plant

This example involves designing a cooling water distribution system to a bank of heat exchangers where we shall use orifice plates to balance the flow distribution. We shall also use the auto sizing functions to develop the system design and size the pipes, pump and orifice plates.

Problem Statement:

It is desired to provide a balanced cooling water flow to four shell and tube heat exchangers HE1, HE2, HE3 and HE4. The size of the heat exchangers has already been determined from the process requirement and is summarized in Table 1.

Table 1: Heat Exchanger Data.

The cooling water is to flow through the heat exchangers and the design system inlet temperature will be 15°C. The design temperature rise of the cooling water across each heat exchanger is 30°C. The elevation of the all elements in this model is zero. The design duty pressure rise for this system is also known, 2.5 bar.

Building the model in the FluidFlow flowsheet:

1. Place two known pressure boundary nodes on the flow sheet.

2. Using the steel pipe element, connect the known pressure boundary nodes together as per Figure 1 below.

3. Add the branch pipe connections, ensuring the branch at each tee junction is assigned correctly.

4. Insert the heat exchangers into each branch line.

5. Insert thin orifice plates into the branch pipe connection serving each heat exchanger.

When complete, the model should appear as per Figure 6.1.1.

The basic model connectivity should appear as set out in Figure 1.

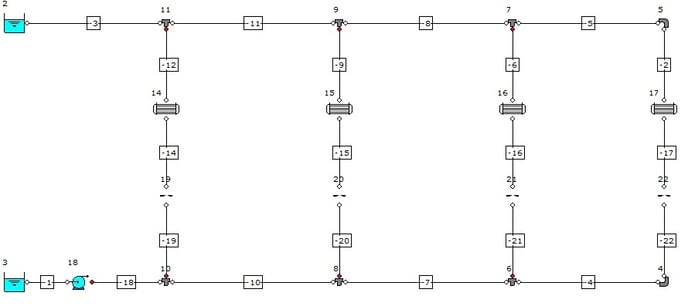
Figure 6.1.1: Base Model.

Each element placed on the flowsheet is provided with default data which the engineer can easily edit based on known design parameters. In this case, we will define the pipe lengths as set out in Table 2. Note, we will accept the default data provided by FluidFlow for the boundary nodes.

Table 2: Pipe Length Data.

Select all the heat exchangers at once by holding the SHIFT key and left mouse-clicking on each. All heat exchangers should now be highlighted on the flowsheet. From the Input tab of the Data Palette, set the Heat Loss Model to Fixed Transfer Rate, the heat transfer direction to Into the Network and the Heat Transfer Unit to kW. We have now set all common parameters for the heat exchangers in one step.

The next step is to define the heat load for each heat exchanger (see Table 1).

The design pump pressure rise is 2.5 bar. We can therefore set the centrifugal pump to Automatically Size from the Input Tab on the Data Palette. In doing so, we have two sizing options available; Size for Flow and Size For Pressure Rise. Select Size For Pressure Rise and defined the Design Pressure Change as 2.5 bar.
Using the data available for the heat exchangers, we can determine the design mass flow rate from the heat balance (Q = m x c x ΔT). The heat transferred to the cooling water will therefore be:

Heat Transferred (W) = mass flow (kg/s) x specific heat capacity (J/kg)  x  temperature rise (°C)

The specific heat of water at 30°C is approx 4154 J/kg, so from Table 1 we see that the mass flow needed to HE1 will be 370000 / (4154 x 30) = 2.969 kg/s. Summarizing in Table 3.

Table 3: Mass Flow Rates.

Since we can auto-size our components, we can define the design flow rate at each orifice plate by setting the Automatically Size option on the Input tab of the Data Palette to On. We now have two sizing models to choose from, Size for Flow and Size for Pressure Loss. As we know the flow rate, select Size for Flow. The next step is to enter the  mass flow rates noted in Table 3 for each orifice plate.

The Sizing Model for pipes is Economic Velocity by default. This means that FluidFlow will determine the Exact Economic Size pipe diameter based on the calculated Economic Velocity.  This velocity is a function of the fluid physical properties, the pipe materials, various capital and installation costs and the operating hours/year. This value is calculated from the Generaux equation and the calculation uses the values and constants stored in the pipe sizing database. Economic velocity is changing (generally decreasing) with time, particularly as energy costs have increased rapidly in recent times. Flite Software keeps these values up to date, which is one of the many reasons you should keep your software current. Economic velocity is meant to be a guide for pipe sizing it is NOT a strict criteria for sizing pipes. For example you would not use this value to size pipes where two phase flow is present, or where plant operation is intermittent, or where materials can degrade at high velocities, or for Non-Newtonian flows.

We wish to develop an efficient system design and as such, we are going to retain the Economic Velocity sizing model.

We are now in a position to calculate the model. The solved system should appear as set out in Figure 6.1.2.

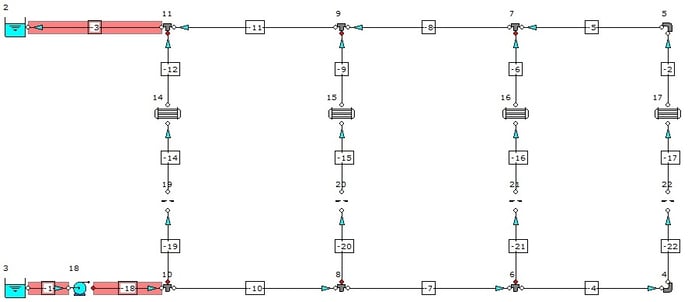
Figure 6.1.2: Solved Model – Default 2 Inch Pipes.

The flow distribution has been shown and if we view the results for any of the four heat exchangers, we can see that the inlet temperature is 15°C and the outlet temperature is 45°C (based on our design 30°C temperature rise).

Note, we also have three warning messages indicating high velocities in the pipelines highlighted in RED.

A quick check on the results for each of the pipes with a high velocity warning indicates velocities in the range of 4.5m/s which is considered high. We therefore need to review the pipe diameter. The diameter of each of these pipes is the default value of 2 inch which is 52.5mm. FluidFlow has determined an economic pipe size of approx. 101mm for each of these three pipes. We therefore need to select the next closest standard size match. Let’s try a 4 inch schedule 40 pipe.

You can multi-select the three pipes by holding the SHIFT key and left mouse-clicking on each pipe. From the Input tab on the Data Palette, access the pipes database and change the pipe to 4 inch schedule 40 pipe. Press Calculate to refresh the results for the system.

If we view the results for the orifice plates, we can see that FluidFlow has automatically determined the K value and the size of orifice required to provide the desired mass flow rate. The pump duty has also been established for us as 9.95 kg/s @ 2.5 bar (26 m fluid).

The warnings have also been corrected and as such, it can be considered that the system is now a relatively efficient design.

Based on the data entry, FluidFlow has therefore automatically sized the pipework, pump and orifice plates for us, thus simplifying the design process and reducing design time considerably.

The final design should appear as set out in Figure 6.1.3.

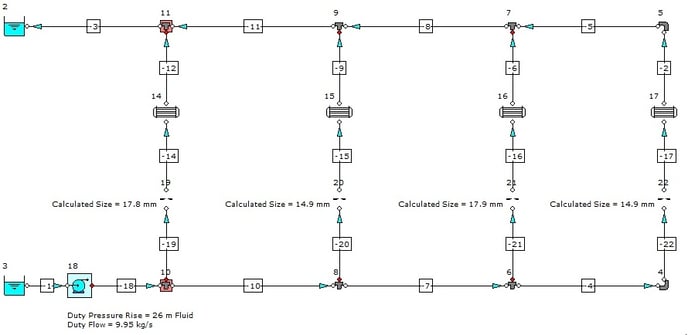
Figure 6.1.3: Solved Model – Updated Pipe Diameters.

Design Note;

When using the auto size function, it’s important not to over-constrain the model as this could lead to model convergence difficulties. For instance, in this example, we could have set the sizing model for the pump to Size for Flow. As we had effectively already defined the total flow in the system by defining the flow rate at each orifice plate, we would have duplicated the flow in the system. It is best to avoid duplicating design parameters when developing your model.

7. Conclusion

FluidFlow has been used by engineers to accelerate the design of process plant and piping systems. The automatic equipment sizing feature has been particularly helpful to the designer as it has been proven to speed up the calculation process and also allows the designer to consider different operating scenarios in an instant.

Occasionally hydraulic calculations for single components are performed by hand which often don’t take into account the effect of the connected pipework and fittings. FluidFlow removes the ambiguity presented by such calculations and helps identify the actual system performance allowing you to spend extra time optimizing plant performance.

If you have a specific design application and wish to use an intuitive user friendly program to speed up your design process, contact us at: support@fluidflowinfo.com.

Testimonial:

“FluidFlow is fast, easy to use, accurate and a reliable package. The software drastically cuts design time - these benefits apply not only to the designer but also to the peer review team. During operation of the built systems, the agreement between running plant pressure readings against design data was highly accurate. That bought my full trust in the package”.

Mat Landowski, Lead Process Engineer