Problem Statement:
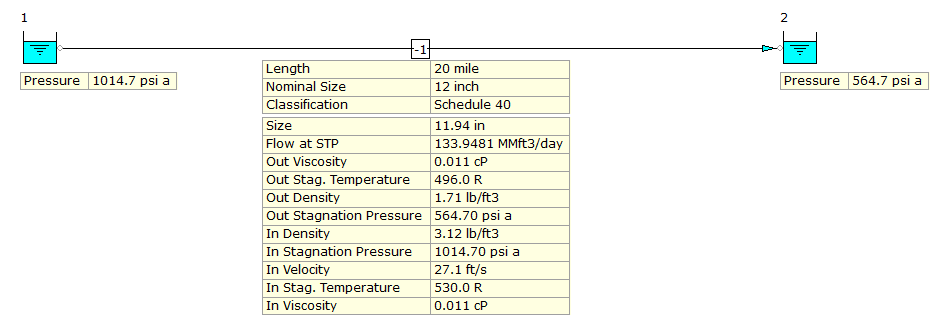
1. Natural gas (T = 530°R inlet / 496°F outlet) is flowing at a steady mass rate through a 12-inch. Schedule 40 steel pipe. Absolute pressure drops from 1014.7 to 564.7 psia in 20 miles of horizontal pipe. Assume the natural gas is pure methane. Calculate the volumetric flow rate in MMSCFD using FluidFlow.
2. Compare the FluidFlow gas calculation result to the following commonly used steady-state compressible flow equations in long pipelines:
- Simplified Isothermal Equation (General Flow Equation)
- Weymouth Equation
- Panhandle A Equation
- Panhandle B Equation
- AGA Equation (fully turbulent flow)
- IGT Equation
3. Assume that the flow of natural gas is incompressible (constant density), isothermal, and follows the Darcy-Weisbach equation, calculate the volumetric flow in MMSCFD.
Solution:
1. The calculated volumetric flow rate of FluidFlow is 133.9 MMSCFD (See the image below):
2. The table below shows the summary of commonly used gas flow equations:
|
Flow Equation |
Description, Applications, and Limitations |
|
Simplified Isothermal Equation |
- The equation is developed from the generalized compressible flow equation by making the following assumptions:
- Easier to solve compared with the adiabatic equations. |
|
Weymouth Equation |
- The Weymouth equation is published in 1912. - Commonly used for sizing gas pipelines and is applicable for fully turbulent flow. - Used for high-pressure high flow rate, and large diameter gas gathering systems. - Does not consider pipe roughness. - Most conservative equation that gives the highest pressure drop for a given flow rate. - Overestimates the pressure drop calculation and because of that it is most frequently used in the design and distribution networks. - Agrees more closely with metered rates than those calculated by most other formulae for short pipelines and gas gathering systems. - Cannot be generally applied to any variety of diameters and roughness, and it is not valid in flow region of partially developed turbulence. |
|
Panhandle A Equation |
- Developed by the Panhandle Eastern Pipe Line Company in the early 1940s. - This equation was developed for natural gas pipelines and it is applicable for partially turbulent (hydraulically smooth) flow. - When “adjusted” with an efficiency factor, E, of about 0.90, the equation reasonably approximates the partially turbulent flow equation. - The equation becomes less accurate the as flow rate increases. - Many users of this equation use an efficiency factor of less than 1 and normally assume a value of 0.92. - Appropriate for moderate gas flow rate operating under medium to high pressure. The values of Reynolds number are in the range of 5 to 11 million and the pressure range of around 800 – 1500 psia. - Generally used for medium to relatively large pipeline diameter value of 12 – 60 inches (305 – 1524 mm). |
|
Panhandle B Equation |
- A new or revised Panhandle Equation was published in 1956 by Panhandle Eastern Pipe Line Company. This revised equation is known as the Panhandle B Equation. - This equation is widely used for large-diameter, high-pressure, long transmission lines and is applicable to fully turbulent flow. - Many users of this equation use an efficiency factor of less than 1 and normally assume a value in the range of 0.88 – 0.94. - In fully turbulent flow, it is found to be accurate for values of Reynolds number in the range of 4 to 40 million. - Applicable to pressure greater than 1000 psia (6895 kPa). - Generally used for larger pipelines greater than 36 inches (914 mm). |
|
American Gas Association (AGA) Equation |
- Developed by the American Gas Association (AGA) in 1964 and 1965. - This equation uses the transmission factor F instead of the friction factor f. - One of the most recommended and used equations for fully turbulent flow. - Able to estimate with high precision flow and pressure drop values, if the pipe roughness is accurately known. - The AGA partially turbulent equation is highly dependent on the Reynolds number and it is used for medium-diameter, medium-flow, and high-pressure systems. - The AGA fully turbulent equation is the most frequently recommended and widely used in high-pressure, high-flow rate systems for medium to large-diameter pipelines. It predicts both flow and pressure drop with a high degree of accuracy if the effective roughness values used in the equation have been measured accurately. |
|
Institute of Gas Technology (IGT) Equation |
- Proposed by the Institute of Gas Technology and is also known as the IGT Distribution Equation. - Does not consider pipe roughness; uses an efficiency factor used on gas distribution piping. - This equation is particularly suitable for high-pressure, high-flow rates through steel or plastic/polyethylene pipes. |
The equations discussed above are commonly encountered in the natural gas industry. These equations assume isothermal flow. The average temperature is used in the equation if the temperature change is defined. These flow-dependent equations, at low flow, are conservative, overpredict pressure drop and underpredict the flow. At high flow, these equations are overly optimistic, underpredict the friction factor, and overpredict the flow. The difference between the equations is where low and high flow is defined.
a. Simplified Isothermal Equation
The calculated volumetric flow rate of Simplified Isothermal Equation using spreadsheet is 139.3 MMSCFD (See the image below):
Results Comparison:
Let us compare the FluidFlow result vs. the Simplified Isothermal Equation result
|
Description |
Unit |
FluidFlow |
Isothermal Equation |
% Difference |
|
Volumetric Flow Rate |
MMSCFD |
133.9 |
139.3 |
3.95% |
Commentary:
The FluidFlow result compare very well with the Simplified Isothermal Equation result. The Simplified Isothermal Equation calculated a flow rate that is more conservative than the FluidFlow result.
b. Weymouth Equation
The calculated volumetric flow rate of Weymouth Equation using spreadsheet is 136 MMSCFD (See the image below):
Results Comparison:
Let us compare the FluidFlow result vs. the Weymouth Equation result:
|
Description |
Unit |
FluidFlow |
Weymouth Equation |
% Difference |
|
Volumetric Flow Rate |
MMSCFD |
133.9 |
136 |
1.56% |
Commentary:
The FluidFlow result compare very well with the Weymouth Equation result. The Weymouth Equation calculated a flow rate that is more conservative than the FluidFlow result.
c. Panhandle A Equation
The calculated volumetric flow rate of Panhandle A Equation using spreadsheet is 171.2 MMSCFD (See the image below):
Results Comparison:
Let us compare the FluidFlow result vs. the Panhandle A Equation result:
|
Description |
Unit |
FluidFlow |
Panhandle A Equation |
% Difference |
|
Volumetric Flow Rate |
MMSCFD |
133.9 |
171.2 |
24.45% |
Commentary:
The FluidFlow result has a large percentage difference compared with the Panhandle A Equation result. The Panhandle A Equation calculated a flow rate that is more conservative than the FluidFlow result.
d. Panhandle B Equation
The calculated volumetric flow rate of Panhandle B Equation using spreadsheet is 168.9 MMSCFD (See the image below):
Results Comparison:
Let us compare the FluidFlow result vs. the Panhandle B Equation result:
|
Description |
Unit |
FluidFlow |
Panhandle B Equation |
% Difference |
|
Volumentric Flow Rate |
MMSCFD |
133.9 |
168.9 |
23.12% |
Commentary:
The FluidFlow result has a large percentage difference compared with the Panhandle B Equation result. The Panhandle B Equation calculated a flow rate that is more conservative than the FluidFlow result.
e. AGA Equation
The calculated volumetric flow rate of AGA Equation using spreadsheet is 139.9 MMSCFD (See the image below):
Results Comparison:
Let us compare the FluidFlow result vs. the AGA Equation result:
|
Description |
Unit |
FluidFlow |
Panhandle B Equation |
% Difference |
|
Volumentric Flow Rate |
MMSCFD |
133.9 |
139.9 |
4.38% |
Commentary:
The FluidFlow result compare very well with the AGA Equation result. The AGA Equation calculated a flow rate that is more conservative than the FluidFlow result.
f. IGT Equation
The calculated volumetric flow rate of IGT Equation using spreadsheet is 166.6 MMSCFD (See the image below):
Results Comparison:
Let us compare the FluidFlow result vs. the IGT Equation result:
|
Description |
Unit |
FluidFlow |
IGT Equation |
% Difference |
|
Volumentric Flow Rate |
MMSCFD |
133.9 |
166.6 |
21.76% |
Commentary:
The FluidFlow result has a large percentage difference compared with the IGT Equation result. The IGT Equation calculated a flow rate that is more conservative than the FluidFlow result
In this example, we introduced the various equations commonly used in compressible flow. In each flow equation, the standard volumetric flow rate at a fixed pressure drop is calculated and compared with the FluidFlow result.
In the figure shown below, we consider a 20 mile long, 12-inch Schedule 40 steel pipe, operating at a fixed pressure drop of 450 psi. The volumetric flow rate is calculated using FluidFlow and different compressible flow equations.
By examining the figure above, it is evident that the highest standard volumetric flow rate is predicted by the Panhandle A equation and the lowest flow rate is predicted by the FluidFlow software. We therefore conclude that the most conservative flow equation that predicts the highest flow rate is the Panhandle A and the least conservative is FluidFlow.
3. The calculated volumetric flow rate assuming the flow is incompressible (constant density), isothermal, and follows the Darcy-Weisbach equation is 155.8 MMSCFD. In the figure below, it can be examined that the calculated flow rate is in between the calculated flow rates of the IGT equation and AGA equation.
The 450-psi pressure drop (∆P) is 44% of the absolute inlet pressure which is 1014.7 psia. According to CRANE Flow of Fluids – Technical Paper No. 410, if the calculated pressure drop is greater than 40% of the absolute inlet pressure, the commonly used compressible flow equations (Isothermal, Weymouth, Panhandle A/B, AGA, etc.) should be used since the flow cannot be treated as incompressible (constant density), and the Darcy-Weisbach equation cannot be applied.
References:
Churchill, S.W., Friction factor equation spans all flow regimes, Chem. Eng. 84 (24) (1977) 91.
Coelho, P.M. and Pinho, C. (2207). Considerations About Equations for Steady State Flow in Natural Gas Pipelines. Journal of the Brazilian Society of Mechanical Sciences & Engineering, 29(3), 262-273.
Crane Co., Flow of fluids through valves, fittings, and pipe, Technical Paper no. 410, 2011.
Hall, Stephen M. (2018). Rules of Thumb for Chemical Engineers (6th Edition) - 4.11 Compressible Flow - Transmission Equations. (pp. 58-71). Elsevier. Retrieved from https://app.knovel.com/hotlink/pdf/id:kt011FN862/rules-thumb-chemical/compressible-flow-transmission
Menon, E.S. (2005). Gas Pipeline Hydraulics (1st ed.). CRC Press. https://doi.org/10.1201/9781420038224
Mohitpour, M., Golshan, H. and Murray, A., 2000, “Pipeline design & construction: A practical approach”, ASME Press.
Schroeder, D. W. 2001, “A tutorial on pipe flow equations”, Paper presented at the PSIG Annual Meeting, Salt Lake City, Utah, October 2001. Retrieved from http://onepetro.org/PSIGAM/proceedings-pdf/PSIG01/All-PSIG01/PSIG-0112/1893397/psig-0112.pdf/1